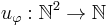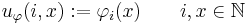utm theorem
In computability theory the utm theorem, or Universal Turing machine theorem, is a basic result about Gödel numberings of the set of computable functions. It proves the existence of a computable universal function which is capable of calculating any other computable function. The universal function is an abstract version of the universal turing machine, thus the name of the theorem.
Rogers equivalence theorem provides a characterization of the Gödel numbering of the computable functions in terms of the smn theorem and the utm theorem.
utm theorem
Let  be a Gödel numbering of the set of computable functions, then the partial function
be a Gödel numbering of the set of computable functions, then the partial function
defined as
is computable.
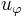 is called the universal function for
is called the universal function for